Силлогизмы архимандрита Евфимия (Вендта) (Богатырев)

← Александр Иосифович Очеретянский 2019-2020

Силлогизмы архимандрита Евфимия (Вендта) автор Михаил Богатырев (р. 1963)

Пометы архимандрита Евфимия на полях публикации В. Н. Лосского «К вопросу об исхождении Святого Духа» 2020 →

Дата создания: 2020. Источник: личная публикация

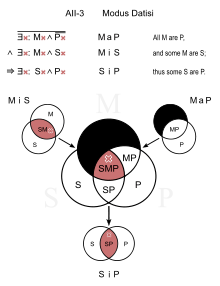
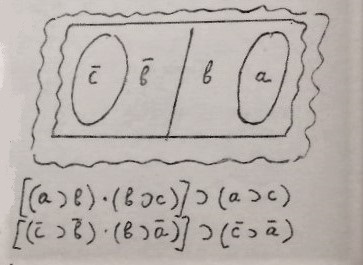Михаил Богатырев

Силлогизмы архимандрита Евфимия (Вендта) <постсиллогизмы>

читать в pdf с илл. (+ приложение "Пометки о. Евфимия на полях публикации В. Н. Лосского)

Отец Евфимий (дата неизвестна, фото из архива В. Н. Платоновой)

Аннотация

Софиологический трактат «Начертание и наречение решений Отрешенного», написанный архимандритом Евфимием (1894, Сергиев Посад — 1973, Муазне, Франция), являет собой беспрецедентную попытку соединить кантианство, схоластику и лингвобогословие, фонетическую заумь и числовую символику, ветхозаветную поэтику и формальную логику. Столь разноплановый материал изложен отцом Евфимием в хаотичной и запутанной манере, что воспринимается как свидетельство божественного Откровения чрезвычайной силы, но, в то же самое время, и как труднопреодолимая преграда в исследовательской работе над трактатом. Стремясь обозначить подходы к интерпретации силлогизмов о. Евфимия, автор данного очерка (гуманитарий по складу ума) вынужден обратиться к азам формально-логического дискурса. Не исключено, что подобным образом – практически «наощупь», отталкиваясь от «нулевого уровня» компетенции – можно вникнуть в некоторые частности, подтвердить или опровергнуть те или иные догадки. Однако для сколько-нибудь грамотной оценки трактата в целом необходим «круглый стол», объединение усилий логиков, лингвистов, философов и богословов.

Исходный материал

Единственный в своем роде представитель «заумного богословия» архимандрит Евфимий (Вендт) обладал математическим складом ума. В начале 1930-х годов в Праге он получил диплом инженера-конструктора, затем закончил Богословский институт, после чего обосновался в Казанском скиту под Парижем, где и священствовал более тридцати лет, вплоть до своей кончины (1973). В написанном им под конец жизни пятисотстраничном трактате «Начертание и наречение решений Отрешенного» отец Евфимий попытался запечатлеть опыт Откровения, пережитый им осенью 1945 года. Стремясь изобразить самую суть Божественных предначертаний, он изобрел своеобразные пиктограммы, включив в них элементы лингвокомбинаторики и теории множеств, богословские термины и космологические метафоры. Один из собеседников отца Евфимия, весьма сочувственно и уважительно к нему относившийся, определял его труд как акт «теолого-лингвистического юродства», своего рода интеллектуальную глоссолалию, не вписывающуюся в общепринятые нормы словесной выразительности.

Чрезвычайно впечатлившись «Критикой чистого разума», архимандрит Евфимий построил собственную систему «архитектоник» на кантианский манер, переводя категории в схемы посредством самобытной «вообразительной» техники. Продолжая исследование законов мышления, начатое еще Аристотелем, Кант объяснял антиномию как противоречие, в которое теоретический разум (Vernunft) впадает сам с собою, пытаясь соотнести идею абсолютного с миром, как с совокупностью всех явлений. Архимандрит Евфимий полагал, что богословие Канта было нацелено на постижение Откровения, а незавершенность его теологической мысли связана с отсутствием в системе немецкого философа представлений о Святой Троице. В примечании к Атласу N°16 отец Евфимий подчеркивал, что рациональная теология Канта в терминах ens originarium (первосущность), ens summum, (высшая сущность) и ens entium (сущность всех сущностей) – «это удивительный максимум того, что можно мыслить, не имея представления о дедукции из Триады». На стр. 59 первого тома своего трактата о. Евфимий пишет:

«Ряды Канта, ведущие к антиномиям, у нас уперты в лицо человека, в лицо его Ангела-Хранителя. Из потенциальной бесконечности (все люди смертны, все бессмертные нечеловечны) – в актуальную (все люди бессмертны, все бессмертные человечны), как показывает последовательность умыслообразов, имеем уравненность судьбы неба и земли в их свободе».

Этот парадокс, сформулированный о. Евфимием (люди смертны — бессмертные нечеловечны; люди бессмертны — бессмертные человечны) словно бы подытоживает ряды силлогизмов, размещенные на стр. 27-35 трактата. Нельзя не отметить то ошеломляющее впечатление, которое производят любые апелляции к науке о законах мышления из уст радикального реформатора самой сути языка, каким, собственно, и был архимандрит Евфимий, с легкостью жертвовавший связностью и внятностью речи ради надежды на верховный смысл, передаваемый заумной лингвокомбинаторикой.

«… Звучит это Онома Имени, Сый-Сын Имени во Им Имя, Свой-Святой. По-Он-Ни-Им-Ма-ние», –

пишет он на стр. 230 второго тома «Начертания...».

В некоторых мистических сочинениях отсутствие логики изложения материала свидетельствует об особенной глубине погружения в проблематику, и трактат отца Евфимия – именно такой случай. Складывается впечатление, что при написании трактата божественное откровение двигало его рукой, не оставляя ему времени на критическое осмысление сказанного, на его оформление, доводку и «разжевывание». В трактате отсутствует какая бы то ни было рубрикация, а некоторое подобие тематического единства сохраняется лишь в череде сквозных изографических построений – атласов и чертежей. Мысль автора с легкостью перелетает (перескакивает!) от одного предмета к другому, и лишь в прописывании «мыслеобразов» – заумных мистико-богословских фонематических вариаций – она становится детальной и скрупулезной. При этом, однако, трактат буквально переполнен апелляциями к формальной логике и теории множеств, диаграммами, построенными на основе кругов Венна etc.

На стр. 247-48 (второй том) архимандрит Евфимий сообщает, что от книги о. Павла Флоренского «Столп и утверждение Истины» он «имел важнейшее внушение», заставившее его обратиться «к изучению Новой Логики».

«Отец Павел приходил <с логикой> как знаток, как мастер с набором инструментов, которыми он пользовался для разверстки содержаний. С дипломом по первому образованию инженера-механика и на шестом десятке жизни я, конечно, не мог продвинуться сколько-нибудь значительно в этом изучении, но <...> восприялся сам зачаток знания в виде tabula exhaustive для двух в составе 16 умыслообразов и таковой же для 256 умыслообразов взаимоотношений трех. <...> Униформа умыслообразов одела энергемы Имени ТроеЛичия. Древние парадигмы оказались громадным современным зданием».

Чтобы двигаться вслед за о. Евфимием далее, необходимо прояснить оставленные им без комментариев детали – в частности, ответить на вопросы, что это за «256 умыслообразов взаимоотношений трех» и т. п. Для этого нам придется обратиться к основам логики.

Краткий экскурс в историю логики

Понятие

Содержание, объем. Типы понятий

Понятием называется форма мышления, которая обозначает собой какой-либо объект или его свойство. В качестве составной части оно входит в другие, более сложные формы мышления – суждение и умозаключение. Содержание понятия – это наиболее важный признак (или признаки) того объекта, который обозначен (выражен) этим понятием. Объем понятия – это количество объектов, охватываемых этим понятием. Например, объем понятия человек гораздо шире, чем объем понятия мужчина, потому что людей существует больше, чем мужчин.

По объему понятия бывают единичными (когда в объем входит только один объект, например: Солнце, город Москва, первый президент России, писатель Лев Толстой ), общими (когда в объем понятия входит много объектов, например: небесное тело, город, президент, писатель ) и нулевыми (когда в объем не входит ни одного объекта, например: Баба Яга, Кащей Бессмертный, Дед Мороз, вечный двигатель, марсианский житель, т. е. понятие существует, а объект, который оно обозначает, не существует).

По объему понятия также бывают собирательными (понятие обозначает объект, который состоит, собирается из какого-то ограниченного набора элементов, делится, распадается на какие-то составные части, например: 10 класс «А», рота солдат, музыкальный коллектив, волчья стая, созвездие) и несобирательными (понятие обозначает объект, который не состоит, не собирается из какого-то ограниченного набора элементов, не делится, не распадается на какие-то составные части, являясь чем-то единым, целым, например: человек, растение, звезда, океан, карандаш).

По содержанию понятия бывают конкретными (понятие обозначает какой-либо объект, например: стол, гора, дерево, планета ) и абстрактными (понятие обозначает не объект, а признак, свойство, например: мужество, глупость, неряшливость, темнота). Также по содержанию понятия бывают положительными (понятие обозначает наличие чего-либо, например: животное, школа, небоскреб, комета) и отрицательными. Понятие считается определенным в том случае, когда у него ясное содержание и резкий объем (например, мастера спорта). Понятие является неопределенным тогда, когда оно имеет неясное содержание и нерезкий объем (например, хороший спортсмен). Обычно понятия делят на сравнимые и несравнимые, совместимые (спортсмен и американец) и несовместимые (ни один треугольник не может быть квадратом и наоборот).

Отношения между понятиями

Совместимые понятия могут быть в отношениях равнозначности, пересечения и подчинения.

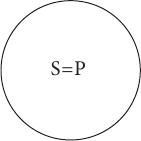
Равнозначность. Например, равнозначными будут понятия квадрат и равносторонний прямоугольник.

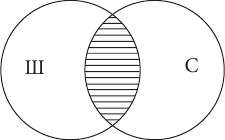
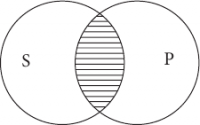
Понятия находятся в отношении пересечения тогда, когда их объемы совпадают только частично (школьник и спортсмен).

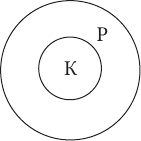
Понятия находятся в отношении подчинения в том случае, когда объем одного из них обязательно больше объема другого и полностью его в себя включает (один объем как бы подчиняется другому). Например, в отношении подчинения находятся понятия карась и рыба, т. к. все караси – это обязательно рыбы.

Отношениями равнозначности, пересечения и подчинения исчерпываются все случаи совместимости между понятиями.

Несовместимые понятия могут быть в отношениях соподчинения, противоположности и противоречия.

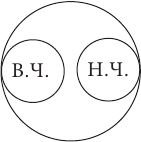
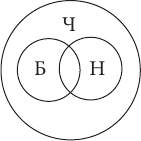
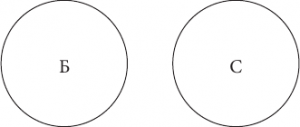
Понятия находятся в отношении соподчинения тогда, когда их объемы не имеют общих элементов, но в то же время входят в объем какого-то третьего понятия, родового для них (совместно ему подчиняются). Например, понятия сосна и береза являются соподчиненными: ни одна сосна не может быть березой и наоборот, но и множество всех сосен, и множество всех берез включается в более широкий объем понятия дерево. На схеме Эйлера отношение соподчинения изображается двумя несоприкасающимися кругами:

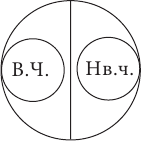
Понятия находятся в отношении противоположности в том случае, если они обозначают какие-то взаимоисключающие признаки, крайние состояния чего-либо, между которыми, однако, всегда есть некий средний, переходный вариант. Например, противоположными являются понятия высокий человек и низкий человек (третьим или переходным вариантом между ними будет понятие человек среднего роста ). На схеме Эйлера отношение противоположности изображается двумя несоприкасающимся кругами, которые находятся как бы на разных «полюсах»:

Понятия находятся в отношении противоречия, если одно из них представляет собой отрицание другого, причем в отличие от противоположных понятий, между противоречащими понятиями никак не может быть третьего или среднего варианта. Например, в отношении противоречия находятся понятия высокий человек и невысокий человек. В том случае, когда одно понятие является отрицанием другого, третий вариант автоматически исключается: и низкий человек , и человек среднего роста – это невысокий человек. На схеме Эйлера отношение противоречия изображается одним кругом, поделенным на две части, которые обозначают противоречащие понятия:

Отношениями соподчинения, противоположности и противоречия исчерпываются все случаи несовместимости между понятиями.

Круговые схемы Эйлера

Как мы уже знаем, в логике выделяется шесть вариантов отношений между понятиями. Два любых сравнимых понятия обязательно находятся в одном из этих отношений. Например, понятия писатель и россиянин находятся в отношении пересечения, писатель и человек – подчинения, Москва и столица России – равнозначности, Москва и Петербург – соподчинения, мокрая дорога и сухая дорога – противоположности, Антарктида и материк – подчинения, Антарктида и Африка – соподчинения и т. д. и т. п.

В начале говорилось о том, что понятия бывают сравнимыми и несравнимыми. Считается, что рассмотренные шесть вариантов отношений применимы только к сравнимым понятиям. Однако возможно утверждать, что все несравнимые понятия находятся между собой в отношении соподчинения. Например, такие несравнимые понятия, как пингвин и небесное тело возможно рассматривать как соподчиненные, ведь пингвин – это не небесное тело и наоборот, но в то же время объемы понятий пингвин и небесное тело входят в более широкий объем третьего понятия, родового по отношению к ним: это может быть понятие объект окружающего мира или форма материи.

Отношения между понятиями боксер, негр и человек изображаются следующей схемой:

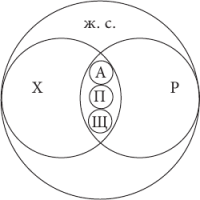
Отношения между понятиями хищник, рыба, акула, пиранья, щука, живое существо изображаются следующей схемой:

Видовые и родовые понятия. Логические операции ограничения и обобщения

Среди различных видов отношений между понятиями следует обратить особенное внимание на отношение подчинения. Как уже говорилось, понятия с меньшим объемом называются видовыми, а понятия с большим объемом – родовыми, причем объем видового понятия всегда полностью включается в объем родового. Видовые и родовые понятия тесно связаны между собой логическими операциями ограничения и обобщения.

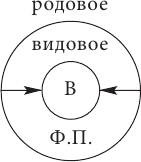
Ограничение понятия – это логическая операция перехода от родового понятия к видовому с помощью прибавления к его содержанию какого-либо признака.

Например, если к содержанию понятия физический прибор прибавить признак «измерять напряжение электрического тока», то оно превратится в понятие вольтметр, которое будет видовым по отношению к исходному родовому понятию физический прибор:

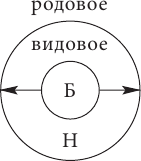
Обобщение понятия – это логическая операция, которая противоположна ограничению и представляет собой переход от видового понятия к родовому с помощью отбрасывания от его содержания какого-либо признака. (Понятно, что содержание понятия, лишенное каких-то признаков, уменьшается, но при этом автоматически увеличивается объем понятия, которое из видового становится родовым или обобщается). Например, если от содержания понятия биология отбросить признак «изучать различные формы жизни», то оно превратится в понятие наука, которое будет родовым по отношению к исходному видовому понятию биология:

Ограничения и обобщения понятий складываются в логические цепочки, в которых каждое понятие (за исключением начального и конечного) является видовым по отношению к одному соседнему понятию и родовым по отношению к другому. Например, если последовательно обобщать понятие Солнце, то получится следующая цепочка:

Солнце → звезда → небесное тело → физическое тело → форма материи

В этой цепочке, как видим, понятие звезда является родовым по отношению к понятию Солнце, но видовым по отношению к понятию небесное тело; так же понятие небесное тело является родовым по отношению к понятию звезда, но видовым по отношению к понятию физическое тело и т. д. Понятно, что движение по нашей цепочке от понятия Солнце к понятию форма материи представляет собой серию последовательных обобщений, а движение в обратном направлении – ограничений. (Если изобразить отношения между понятиями из указанной цепочки на схеме Эйлера, то получатся круги, последовательно располагающиеся один в другом: самый маленький обозначает понятие Солнце, а самый большой – форма материи).

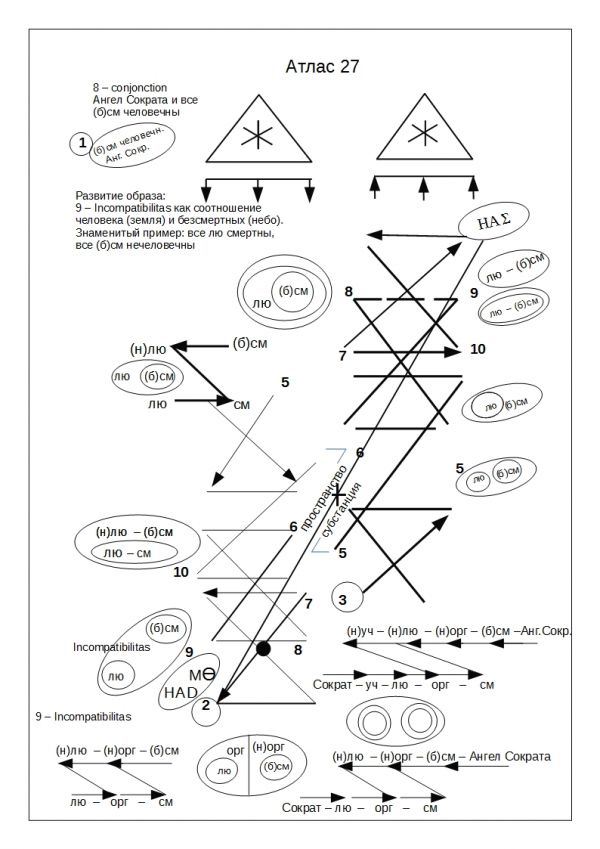
У архимандрита Евфимия в Атласе 27 (см. далее) приведена логическая цепочка последовательного обобщения понятия Сократ :

Сократ → учителя → люди → организмы → смертные

Итак, почти любое понятие можно как ограничить, так и обобщить. Это значит подобрать для него как видовое понятие, так и родовое. Например, ограничением понятия человек будет понятие спортсмен (или писатель, или мужчина, или молодой человек и т. п.), а его обобщением будет понятие живое существо:

Существуют также логические операции сложения и умножения понятий. При сложении образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий (этот результат называют логической суммой). При умножении образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий (этот результат называют логическим произведением).

Результатом умножения соподчиненных понятий береза и сосна является нулевое понятие (т. е. логическое произведение понятий береза и сосна представляет собой пустое множество – не существует ни одной березы, которая могла бы быть сосной и наоборот):

Как правило, в естественном языке (т. е. том, на котором мы общаемся) результат сложения понятий выражается союзом «или», а умножения – союзом «и». Но [Свинцов 1998, 60–61] указывает на многозначность этих союзов, «способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями».

«Удачна ли, в частности, – спрашивает он, – следующая формулировка одного из правил пользования городским транспортом: «Безбилетный проезд и бесплатный провоз багажа наказывается штрафом»? Представим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них войдут пассажиры, не взявшие билета, в другое – не оплатившие провоз багажа. Если союз «и» рассматривать как показатель логического умножения, то придется признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но все же использование союза «или» здесь следует признать предпочтительным».

Суждение

Субъект, предикат, связка

Суждение – это более сложная форма мышления по сравнению с понятием (оно состоит из понятий, связанных между собой и что-либо утверждает или отрицает, например: Все треугольники не являются квадратами). Неудивительно поэтому, что суждение имеет определенную структуру, в которой можно выделить четыре части.

1. Субъект (обычно обозначается латинской буквой S) – это то, о чем идет речь в суждении. Например, в суждении: «Все учебники являются книгами» речь идет об учебниках, поэтому субъектом данного суждения выступает понятие учебники.

2. Предикат (обычно обозначается латинской буквой Р) – это то, что говорится о субъекте. Например, в том же суждении: «Все учебники являются книгами» о субъекте (т. е. об учебниках) говорится, что они – книги, поэтому предикатом данного суждения выступает понятие книги .

3. Связка – это то, что соединяет субъект и предикат. В роли связки могут быть слова есть, является , это и т. п.

4. Квантор – это указатель на объем субъекта. В роли квантора могут быть слова все, некоторые, ни один и т. п. Рассмотрим суждение: «Некоторые люди являются спортсменами». В нем субъектом выступает понятие люди, предикатом – понятие спортсмены, роль связки играет слово «являются», а слово «некоторые» представляет собой квантор. Если даже в каком-то суждении (выраженном в форме предложения) отсутствует связка или квантор, то они все равно там подразумеваются. Например, в суждении: «Тигры – это хищники» квантор отсутствует, но он подразумевается – это слово «все».

С помощью условных обозначений субъекта и предиката у любого суждения можно отбросить его содержание и оставить только его логическую форму. Например, если у суждения: «Все прямоугольники – это геометрические фигуры» отбросить содержание и оставить форму, то получится: «Все S есть Р». Точно так же логическая форма суждения: «Некоторые животные не являются млекопитающими» – «Некоторые S не есть Р».

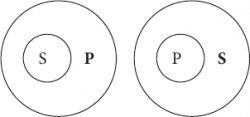
Отношения между субъектом (S) и предикатом (Р)

Между субъектом и предикатом любого суждения, всегда представляющими какие-либо понятия, существуют следующие отношения.

1.Равнозначность. В суждении: Все квадраты – это равносторонние прямоугольники субъект (квадраты) и предикат (равносторонние прямоугольники) находятся в отношении равнозначности, потому что представляют собой равнозначные понятия (квадрат – это обязательно равносторонний прямоугольник, а равносторонний прямоугольник – это обязательно квадрат).

2. Пересечение. В суждении: Некоторые писатели – это американцы субъект (писатели) и предикат (американцы) находятся в отношении пересечения, т. к. являются пересекающимися понятиями (писатель может быть американцем и может им не быть, и американец может быть писателем, но также может им не быть).

3. Подчинение. В суждении: Все тигры – это хищники  субъект (тигры)  и предикат (хищники)  находятся в отношении подчинения, потому что представляют собой видовое и родовое понятия (тигр – это обязательно хищник, но хищник – не обязательно тигр). Также в суждении: Некоторые хищники являются тиграми  субъект (хищники ) и предикат (тигры ) находятся в отношении подчинения, будучи родовым и видовым понятиями. Понятно, почему в случае подчинения между субъектом и предикатом суждения возможны два варианта отношений: объем субъекта полностью включается в объем предиката или наоборот.

4. Несовместимость. В суждении: Все планеты не являются звездами  субъект (планеты ) и предикат (звезды)  находятся в отношении несовместимости, т. к. являются несовместимыми (соподчиненными) понятиями (ни одна планета не может быть звездой, и ни одна звезда не может быть планетой).

Виды простых суждений. Логический квадрат

Простые суждения (т. е. имеющие в своем составе один субъект и один предикат) по объему субъекта и качеству связки делятся на 4 вида. Объем субъекта может быть общим (все) и частным (некоторые), а связка может быть утвердительной (есть, или является) и отрицательной (не есть, или не является). Это наглядно представлено в следующей простой таблице.

Соответственно, можно выделить только четыре комбинации, которыми исчерпываются все виды простых суждений:

1. Общеутвердительные суждения. Как явствует из названия, это суждения с общим объемом субъекта и утвердительной связкой: Все S есть Р, например: Все школьники являются учащимися. Эти суждения обозначаются в логике латинской буквой А.

2. Частноутвердительные суждения. Название данного вида свидетельствует о том, что он представляет собой суждения с частным объемом субъекта и утвердительной связкой: Некоторые S есть Р, например: Некоторые животные являются хищниками. Эти суждения обозначаются латинской буквой I. 3. Общеотрицательные суждения – это суждения с общим объемом субъекта и отрицательной связкой: Все S не есть Р (или Ни одно S не есть Р), например: Все планеты не являются звездами (или Ни одна планета не является звездой). Такие суждения обозначаются латинской буквой Е.

4. Частноотрицательные суждения – это суждения с частным объемом субъекта и отрицательной связкой: Некоторые S не есть Р, например: Некоторые грибы не являются съедобными. Эти суждения обозначаются латинской буквой О.

Логический квадрат (источник – [Радлов 1900])

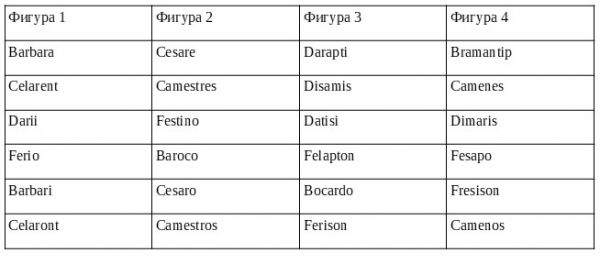
Авторству византийского ученого Михаила Пселла (XI в.) принадлежит так называемый «логический квадрат», в котором наглядно выражается отношение различных видов суждений. Ему же принадлежит и общеупотребительное обозначение буквами количества и качества суждений (а, е, i, о). Эти буквы взяты из двух латинских слов: AFFIRMO – утверждать и NEGO – отрицать. Кроме того, Пселл изобрел мнемонические кодовые имена различных modi (греч. τρόποι) фигур силлогизмов; латинские названия видов фигур, приводимые в формальных логиках (Barbara, Darii etc), взяты у Петра Испанского (папы Иоанна XXI), который комментировал и правил сочинения Пселла.

Одна из современных версий «логического квадрата»

Аристотель. Древо Порфирия

В нескольких трактатах, объединенных его последователями под общим названием «Органон», Аристотель сформулировал основы логики и, в частности, теорию построения правильных (дедуктивных) рассуждений, позволяющих из истинных высказываний гарантированно получать истинные следствия. Неоплатоник Порфирий во «Введении» к аристотелевым «Категориям» (Κατεγορίαι, Praedicamenta) наметил иерархическую схему предикатов, представленную впоследствии в виде «древа» (arbor Porphyriana).

Схема родовидового деления категории «субстанция» из издания латинского
комментированного перевода Порфириева «Введения», выполненного Боэцием (источник файла: I.R. Annie IP)

Arbor Porphyriana является схемой подчинения и соподчинения понятий (многоступенчатую субординацию родовых и видовых понятий при дихотомическом делении). [Стяжкин 1967, 93] пишет: «На вершине “древа” помещается самое широкое по объему понятие “высший род“ (genus generalissimum), в самом низу “древа” находится “низший вид” (infinima species). Узлы соответствуют понятиям, линии между узлами – отношениям между ними (типа подчинения менее широкого по объему понятия понятию с большим объемом). Древо Порфирия – это схема со строгой иерархией, т. е. в ней нет такого положения, при котором какое бы то ни было понятие на “древе” оказалось бы подчинено более чем одному другому понятию».

Дихотомическое деление понятий (Боэций?)

Версия arbor Porphyriana

Ещё одна версия arbor Porphyriana

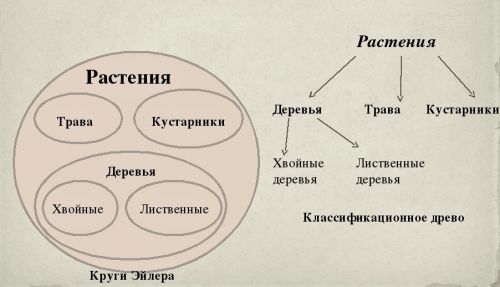
Отметим, что с оглядкой на графические особенности arbor Porphyriana самая, пожалуй, сложная и запутанная схема архимандрита Евфимия – Атлас 28 – приобретает черты осмысленности:

«Начертание...», т.1, с. 30. Атлас 28 (перерисованный нами нижний лист; фрагм.)

Классификационное древо моделирует родо-видовую иерархию и выявляет отношения подчинения, а отношения объемов лучше выявляются с помощью кругов Эйлера:

Категория «субстанция» в примере Порфирия является наивысшим родом, по признакам «телесное» и «бестелесное» она делится на два вида — «телесная субстанция» (substantia corporea), т. е. тело, и «бестелесная субстанция» (incorporea). «Тело» (corpus), рассматриваемое как род, делится по признакам «одушевлённое» и «неодушевлённое» на виды «одушевлённое тело» (corpus animatum), т.е. организм, и «неодушевлённое тело» (corpus inanimatum). «Организм» по признакам «чувствующий» и «нечувствующий» (sensibile / insensibile) делится на виды «животное» (animal) и «растение» (?). «Животное», рассматриваемое как род, делится на виды «разумное существо» (animal rationale), т.е. человек, и «неразумное существо» (animal irrationale). «Человек» (homo) является в данной последовательности понятий низшим понятием и уже не может рассматриваться как род и делиться на виды, а является совокупностью индивидов, то есть совокупностью частностей, которые не могут рассматриваться как понятия (в примере Порфирия — Платон, Сократ).

Развитие систематики Порфирия Петром Испанским (папой Иоанном XXI):
десять отношений между пятью предикатами

«Начертание...», т. 1, с. 31 (оригинал)

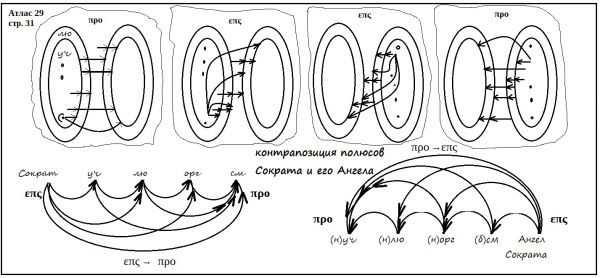
Некоторые элементы графической организации Атласа 29 наводят на мысль о том, что отец Евфимий изучал средневековую схоластику, и в частности, труды Петра Испанского (см. выше).

«Начертание...», т.1, с. 31. Атлас 29 (фрагм., перерисованный нами)

Атлас 29 концептуально нагружен терминами традиционной логики и кантианской философии. Извлеченное из средневековой латыни ens обозначает сущность (например, ens rationis – абстрактная логическая сущность; ей противопоставляется ens reale – сущность, имеющая фактическое или потенциальное существование за пределами ограниченного разума). Pro – от др.-греч. πρό – движение вперед, предпочтение, последующее по времени, в пользу дела (в отличие от префикса анти-). Итак, на Атласе представлена «контрапозиция полюсов Сократа и его Ангела» в регистре между ens и pro.

«В классической логике контрапозиция понимается как сложная логическая операция, используемая и в логике предикатов, и в логике высказываний, включающая не только отрицание, но и обмен позициями терминов или высказываний. Так, в классической силлогистике различают (1) контрапозицию предикату, (2) контрапозицию субъекту и (3) чистое противопоставление. Например, для общеутвердительных высказываний они проводятся по формулам:

Всякий S есть Р ↔ Всякий не-Р не есть S (1) Всякий S есть Р ↔ Некоторый Р есть не-S (2) Всякий S есть Р ↔ Всякий не-Р есть не-S (3).

Здесь S – субъект простого категорического высказывания, Р – его предикат, а знак ↔ является обозначением двустороннего отношения логической выводимости».

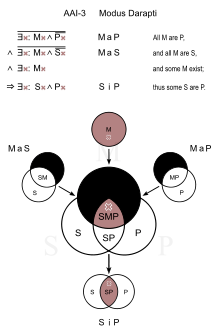
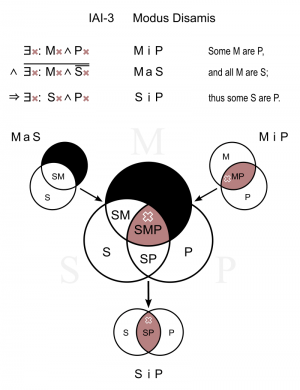
Диаграммы Эйлера и Венна

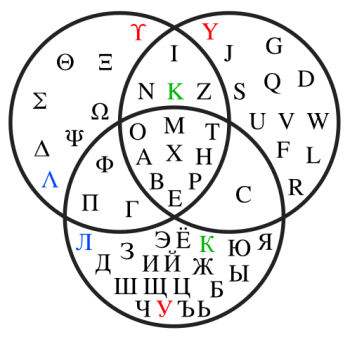
Александрийский богослов-монофизит Иоанн Филопон (VI век), комментируя Аристотеля, впервые применил для иллюстрации силлогистических закономерностей идеографические средства (незамкнутые дуги), предвосхитив диаграммы Лейбница и Эйлера. Отметим, что во многих схолиях архимандрита Евфимия (в особенности на стр. 500-550 второго тома трактата «Начертание...», где оформлены результаты «побуквенной счетности по образцу матемологическому») фигурируют круги Венна, основанные на существенно иной идее, нежели диаграммы Эйлера, базирующиеся на силлогистике Аристотеля. Круги Венна были созданы для решения задач математической логики: «их основная идея разложения на конституенты возникла на основе алгебры логики».

Диаграмма Венна, показывающая все пересечения
греческого, русского и латинского алфавитов (буквы заглавные)

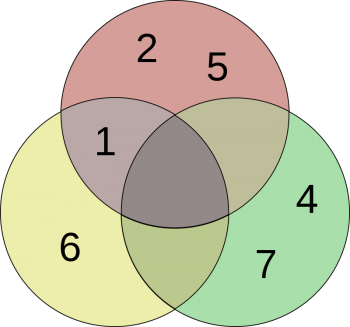
На диаграммах Эйлера непересекающиеся (или дизъюнктные) множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами. Ниже даны диаграммы Венна и Эйлера для 3 множеств однозначных натуральных чисел: A = { 1 , 2 , 5 }; B = { 1 , 6 }; C = { 4 , 7 }.

Диаграмма Эйлера

Диаграмма Венна

«Начертание...», т. 2, с. 165. Фонемная комбинаторика и диаграммы о. Евфимия
(в Букваре о. Евфимия звуки ч, ц и некоторые другие заменены на универсальную буквенную категорию «тсг»)

Аристотель считал, что душа и тело не являются составными элементами «я»; душа есть сила, действующая посредством тела, а тело — естественное орудие души. Они неразделимы, как глаз и зрение, и в этом смысле, добавим, единосущны. Подобно тому, как для закручивания шурупов используется отвертка с наконечником, соответствующим рисунку на шляпке, так и каждой данной душе, по Аристотелю, соответствует определенное тело (ὄργανον — organon — по-гречески означает орудие, инструмент). Очевидно, что идея перевоплощения, восходящая к пифагорейскому учению о переселении душ, в котором можно усмотреть ключ к идеализму Платона, была Аристотелю абсолютно чужда. В отличие от натурфилософов Аристотель рассматривал тело как энтелехию души, как результативную составляющую некоторого «энергоемкого» процесса, отрицая при этом возможность существования души вне тела. Следовательно, Аристотелево единосущие исключает и Вечную жизнь. У его онтологического тумблера всего два положения: «бытие» и «небытие».

Складывается впечатление, что от аристотелева рационализма в опытах архимандрита Евфимия остается лишь оболочка, заполняющаяся разнообразными флуктуациями «изъяснения неизъяснимого».

«<...> некоторые смертные суть не организмы, некоторые смертные не суть не организмы, некоторые не организмы не суть смертны,  некоторые не организмы смертны <...>», –

пишет о. Евфимий в Атласе N°28. Поиски достоверного контекста для данного комплекса утверждений вынуждают нас обратиться к тематике противопоставления души и материального мира перед лицом Царствия Небесного (ведь в противном случае высказывания типа «некоторые смертные суть не организмы» пришлось бы отнести к разряду неправильных). Так значит, речь идет о душе и о Вечной жизни, а под смертным не-организмом следует подразумевать смертный грех? Очевидно, что этом пункте установки архимандрита Евфимия идут вразрез с воззрениями греческого философа-рационалиста.

Силлогизмы

Четыре фигуры и 256 модусов

Силлогизм в самом общем случае — это вид рассуждения, в котором две посылки, связывающие субъекты (подлежащие) и предикаты (сказуемые), объединены общим (средним) термином, обеспечивающим замыкание понятий (терминов) в заключении.

В простом категорическом силлогизме содержатся три термина: S — меньший термин: субъект заключения (аналог подлежащего; входит в меньшую посылку и в заключение); P — бо́льший термин: предикат заключения (аналог сказуемого; входит в бо́льшую посылку и в заключение); M — средний термин: входит в обе посылки, но не входит в заключение. Термины силлогизма попарно связаны в высказываниях посредством одного из следующих четырёх логических отношений:

всякое X есть Y, ни одно X не есть Y, некоторые X есть Y, некоторые X не есть Y.

Различают три типа связи между подлежащим и сказуемым: тождество, подчинение, отношение.

Как уже говорилось выше, четыре вида простых атрибутивных высказываний получили специальные обозначения: A (от латинского слова affirmo) — общие высказывания; I (от affirmo) — частно-утвердительные высказывания; E (от лат. nego) — обще-отрицательные высказывания; O (от nego) — частно-отрицательные высказывания.

Для характеристики соотношения объемов субъекта и предиката используется понятие распределенность термина. Термин считается распределенным, если его объем полностью включается в объем другого термина или полностью исключается из него. Термин считается нераспределенным, если его объем лишь частично включается в объем другого термина или частично исключается из него. Распределенность терминов силлогизма имеет следующие правила:

a) субъект всегда распределен в общем высказывании и никогда не распределен в частном высказывании;

b) предикат всегда распределен в отрицательных суждениях, в утвердительных он распределен тогда, когда по объёму Р ⇐ S;

c) в качестве предиката (в некоторых случаях) может выступать субъект;

d) единичные высказывания (такие, в которых субъект является единичным термином) приравниваются к общим.

Фигуры силлогизмов

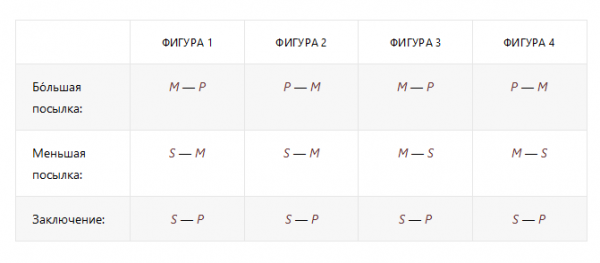
Согласно указанным условиям силлогизмы делятся на так называемые фигуры, которые представляют собой множество простых категорических силлогизмов, имеющих одну и ту же структуру, определяемую расположением среднего термина (M) в посылках.

Каждой фигуре соответствуют модусы, различающиеся в зависимости от логических отношений, связывающих термины в высказываниях силлогизма. Модусом простого силлогизма называется набор простых суждений, входящих в силлогизм. Модус простого силлогизма составляет три суждения. Например,

Все небесные тела движутся. Все планеты — это небесные тела. — Все планеты движутся.

Этот силлогизм имеет модус ААА (здесь первая посылка — это простое суждение вида A, и вывод в данном случае представляет собой простое суждение вида A). Пример модуса АЕЕ:

Все журналы — это периодические издания. Все книги не являются периодическими изданиями. — Все книги не являются журналами.

Пример модуса ААI:

Все углероды — это простые тела. Все углероды являются электропроводными. — Некоторые электропроводники — простые тела.

В каждой фигуре — 64 модуса. Соответственно, во всех четырех фигурах силлогизмов насчитывается 256 модусов — вот они «256 умыслообразов взаимоотношений трех», как пишет отец Евфимий на стр. 248 второго тома своего трактата (подразумевается, что в простом категорическом силлогизме содержатся три термина, S, P и M). Однако из всех этих 256 модусов только 24 дают достоверные выводы. Это те модусы, для которых между посылками и заключением существует отношение логического следования. Эти 24 модуса называются правильными. Остальные модусы приводят к вероятностным выводам и называются, соответственно, неправильными.

Существуют несколько методов проверки силлогизмов. Аристотель и его средневековые последователи постулировали логическую корректность модусов первой фигуры, правильные модусы других фигур обосновывались посредством сведéния к модусам первой фигуры с использованием процедур обращения высказываний, перестановки посылок, законов логического квадрата и рассуждения от противного. Семантическая проверка силлогизма осуществляется с помощью объёмных диаграмм — кругов Эйлера.

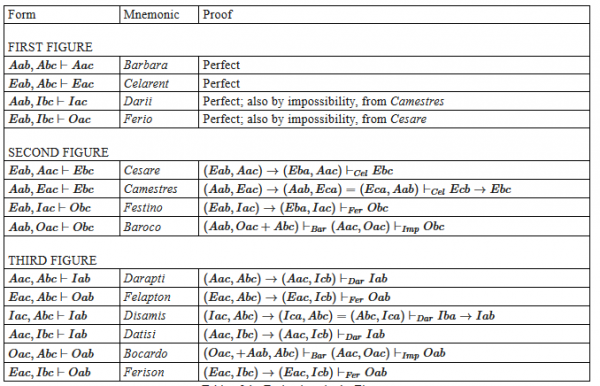
В традиционной силлогистике для 24 правильных модусов каждой фигуры имеются мнемонические имена. В этих названиях (см. таблицу ниже) гласные буквы слева направо указывают тип большей, меньшей посылок и заключения.

Мнемонические имена 24 правильных модусов аристотелевой аналитики

В другом источнике (Стенфордская Энциклопедия) в отдельную таблицу сведены 14 «дедуктивных» модусов. Robin Smith пишет: «В Первой аналитике (Ἀναλυτικὰ πρότερα, Analytica priora), I. 4–6, Аристотель показал, что некоторые комбинации предпосылок (см. таблицу ниже), строятся на дедукции, а все другие комбинации предпосылок – не дедуктивны. Знак «⊢» в таблице отделяет посылки от заключения; он может быть заменен словом «поэтому». Во второй колонке указаны имена (Barbara, Darii, etc), присвоенные в Средние века выводам в доказательствах Аристотеля (эти мнемонические ключи широко используются и сегодня). В третьей колонке кратко изложена процедура, с помощью которой Аристотель получил данный вывод».

Фигуры дедукции (Table of the Deductions in the Figures)

Так, в частности, Bocardo ключает бо́льшую посылку типа O, меньшую посылку типа A и вывод типа O, то есть конкретную отрицательную бо́льшую посылку, утвердительную универсальную меньшую посылку и конкретный отрицательный вывод.

Cиллогизм в Bocardo состоит из предложения следующего типа: некоторые P не S, но все P суть F, поэтому некоторые F не S: «Некоторые утки не летают; Все утки – птицы; Есть птицы, которые не летают».

Примеры силлогизмов каждого типа

Barbara

Все животные смертны. Все люди — животные. — Некоторые электропроводники — простые тела.

Celarent

Ни одна рептилия не имеет меха. Все змеи — рептилии. – Ни одна змея не имеет меха.

Darii

Все котята игривые. Некоторые домашние животные — котята. – Некоторые домашние животные — игривые.

Ferio

Ни одна домашняя работа не весела. Некоторое чтение — домашняя работа. – Некоторое чтение не весело.

Barbari

Все животные смертны. Все люди — животные. – Некоторые люди смертны.

Celaront

Ни одна рептилия не имеет меха. Все змеи — рептилии. – Некоторые змеи не имеет меха.

Cesare

Ни одна здоровая еда не полнит. Все торты полнят. – Ни один торт не здоровая еда.

Camestres

Все лошади имеют вздутие живота. Ни один человек не имеет вздутия живота. – Ни один человек не лошадь.

Festino

Ни один ленивый человек не сдает экзамены. Некоторые студенты сдают экзамены. – Некоторые студенты не ленивы.

Baroco

Все информативные вещи полезны. Некоторые сайты не полезны. – Некоторые сайты не информативны.

Cesaro

Ни одна здоровая еда не полнит. Все торты полнят. – Некоторые торты не являются здоровой едой.

Camestros

Все лошади имеют вздутие живота. Ни один человек не имеет вздутия живота. – Некоторые люди не лошади.

Darapti

Все фрукты питательны. Все фрукты вкусны. – Некоторые вкусные продукты питательны.

Disamis

Некоторые кружки красивы. Все кружки полезны. – Некоторые полезные вещи красивы.

Datisi

Все прилежные мальчики в этой школе рыжие. Некоторые прилежные мальчики в этой школе — пансионеры. – Некоторые пансионеры в этой школе рыжие.

Felapton

Ни один кувшин в этом шкафу не нов. Все кувшины в этом шкафу треснутые. – Некоторые треснутые вещи в этом шкафу не новы.

Bocardo

Некоторые кошки бесхвосты. Все кошки — млекопитающие. – Некоторые млекопитающие бесхвосты.

Ferison

Ни одно дерево не съедобно. Некоторые деревья зелёные. – Некоторые зелёные вещи не съедобны.

Bramantip

Все яблоки в моём саду полезны. Все полезные фрукты зрелы. – Некоторые зрелые фрукты — яблоки в моём саду.

Camenes

Все яркие цветы ароматны. Ни один ароматный цветок не выращен в помещении. – Ни один выращенный в помещении цветок не ярок.

Dimaris

Некоторые небольшие птицы питаются мёдом. Все питающиеся мёдом птицы цветные. – Некоторые цветные птицы небольшие.

Fesapo

Ни один человек не совершенен. Все совершенные существа мифические. – Некоторые мифические существа не люди.

Fresison

Ни один компетентный человек не ошибается. Некоторые ошибающиеся люди работают здесь. – Некоторые работающие здесь люди некомпетентны.

Camenos

Все яркие цветы ароматны. Ни один ароматный цветок не выращен в помещении. – Некоторые выращенные в помещении цветы не ярки.

Категории

Согласно «Философскому словарю» Конт-Спонвиля, категории (сatégories) – это наиболее общие предикаты, которые в рамках суждения можно присвоить тому или иному субъекту: фундаментальные понятия, позволяющие осмыслить бытие (Аристотель) или структурировать мысль (Кант). Оба эти варианта применения категорий не столько противостоят друг другу, сколько дополняют друг друга: второе делает возможным первое, первое оправдывает второе. «Если бы наша мысль осмысливала только себя самое, – добавляет Андре Спонвиль, – мы были бы Богом или сумасшедшими. И в том и в другом случае нам незачем было бы мыслить».

Аристотель выделяет 10 категорий, каждая из которых представляет собой один из способов выразить бытие (поскольку «бытие выражается в нескольких смыслах»): субстанция, количество, качество, отношение, место, время, положение, обладание, действие, страсть. Кант ссылается на Аристотеля, но выделяет 12 категорий, соответствующих логическим функциям суждения, которые он группирует по три: категории количества (единство, множественность, совокупность); качества (реальность, отрицание, ограничение); отношения (присущность и самостоятельное существование, причинность и зависимость, общение или взаимодействие), наконец, категории модальности (возможность и невозможность, существование и несуществование, необходимость и случайность). По Аристотелю, это роды бытия, по Канту – чистые понятия рассудка.

Кант называл категории «онтологическими предикатами», указывая, что их логическая работа заключается в том, что они используются в качестве сказуемых объектов.

С понятием категории связано понятие категоричности (сatégorique), обозначающее безусловное утверждение или отрицание, исключающее альтернативу. Категорическое суждение – это суждение, не являющееся ни гипотетическим, ни разделительным. Например: «Сократ – человек». Или: «Этот человек – не Сократ».

Отсюда Кант выводит понятие категорического императива – абсолютного требования, не зависящего от условий и не признающего отговорок (например, «не лги»). Все категорические императивы в конечном счете сводятся к одному-единственному, который звучит так: «Поступай только согласно такой максиме, руководствуясь которой ты в то же время можешь пожелать, чтобы она стала всеобщим законом» («Основы метафизики нравственности», раздел II).

Более развернутое определение категории дает В. А. Эдельман: «Категория — это предельно общее фундаментальное понятие, выражающее наиболее существенные отношения тех или иных областей действительности, знания и деятельности. Образуется как последний результат абстрагирования от предметов и их особенных признаков. К категориям относятся предельно широкие по-своему объему понятия, то есть те, для которых не существует более общего, родового понятия. Таким образом, основное свойство категорий заключается в определении наиболее фундаментальных и широких классов сущностей. Будучи универсальными формами мышления, категории воспроизводят свойства и отношения бытия и познания во всеобщем и наиболее концентрированном виде, и имеют априорное значение в качестве универсалий и предельных понятий».

Категории у Аристотеля

Как сказано выше, Аристотель выявил десять высших категорий (родов) сущего:

Субстанция — сущность, первооснова предмета (substantia).
Количество (сколько) — пространственно-числовые (количественные) характеристики предмета (quantitas).
Качество (какое) — неколичественные (качественные) свойства предмета (qualitas).
Отношение — способ, которым один предмет может быть связан с другим (relatio).
Пространство (где) — положение предмета относительно ближайшего окружения (situs).
Время (когда) — положение предмета относительно последовательности событий (quando).
Состояние (ситуация) — положение частей предмета друг относительно друга (ubi).
Обладание — наличие постоянного внешнего обстоятельства предмета (habitus).
Действие — произведение изменения в некотором другом предмете (actio).
Претерпевание — принятие изменения от некоторого другого предмета (passio).
(Аристотель. «Категории», lb–2а).

Категории у Аристотеля — это схемы высказываний: то, что высказывается о сущем, подпадает под ту или иную категорию. Поэтому категории характеризуют классы высказываний, независимые друг от друга и определяющие различные способы осмысления бытия. Функция категорий заключается не в том, чтобы охарактеризовать онтологическую структуру бытия (этот ход мысли возникнет позднее — при онтологизации категорий как родов сущего), а в том, чтобы служить гарантом правильно выбранной стратегии аргументации и доказательства, наложить запреты на подмену одних смыслов другими. Аристотель проводит различие между классификацией предикатов по категориям и по предикабилиям, то есть по типам предикатов (род, вид, собственное отличие, случайное или привходящее отличие). Каждая из этих предикабилий относится к одной из категорий как видовое к родовому («Топика», IX 103b 25), например, «человек» — к «сущности», «белый цвет» — к «качеству», и так далее. Кроме того, субъект и предикат суждения должны принадлежать к одной категории (Аристотель. Вторая аналитика. 103b. 20–35). Так, суждение «Человек есть белый цвет» ложно уже потому, что нарушает это требование. Отсюда следует, что не только типов понятий, но и типов суждений существует ровно столько же, сколько и категорий. Наиболее существенной оказывается классификация по категориям. Проблема полноты категорий, возникшая перед Аристотелем, связана с полнотой описания типов языковых высказываний, с различением осмысленных и бессмысленных высказываний, с анализом способов аргументации в ответах на вопросы, имеющей большое значение для учения о категориях.

Категории у cтоиков и неоплатоников

Стоики значительно упростили аристотелевскую таблицу, оставив в ней только четыре категории: «субстрат» (субстанция), «качество», «образ существования» (как) и «отношение» (то, по отношению к чему). При этом категории понимались как способы конструирования сущего и любых форм проявления первой сущности — «материи»: 1) бескачественной материи; 2) преобразующей силы; 3) свойств; 4) отношений. Плотин в первых трех трактатах VI «Эннеады» дал критику аристотелевского и стоического учений о категориях, доказывая необходимость разделения категорий на умопостигаемые и чувственные, признавая первые образцом для вторых, и формулирует первые (как у Платона) в виде «сущего», «движения», «покоя», «тождества» и «различия», а чувственные категории — как «субстанцию», «отношение», «количество», «качество», «движение».

В средневековой философии креационистский способ мысли задает принципиально иной подход к категориям и их субординации, чем в античной философии, хотя в Средние века комментарии к «Категориям» Аристотеля были весьма распространены. Ученик Плотина Порфирий написал «Введение в категории Аристотеля», имевшее широкое распространение в течение всего Средневековья наряду с «Категориями» Аристотеля. Здесь обозначены пять категорий: «род», «вид», «видовое различие», «собственный признак» и «привходящий признак». Но каково их отношение к категориям Аристотеля, об этом у Порфирия ничего не говорится. Пять категорий Порфирия даны в плане описательного анализа и многочисленных различений. Тем самым учение о категориях сужается и рассматривается лишь через призму родо-видовых отношений, хотя без знания рода и вида нельзя понять категории.

Категории у Боэция

Боэций видит в десяти категориях наивысшие роды сущего, «роды вещей, с которыми сталкивается ум в процессе мышления или рассуждающий человек в разговоре» ([Боэций 1990, 12] – Боэций. Утешение философией и другие трактаты. – М., 1990, с. 12). Вместе с тем категории – это высшие роды обозначений (genera significationum). Бесконечно число вещей и возможность обозначений. Все возможное знание постигается и упорядочивается тропами, в которые могут входить категории, однако это не относится к познанию Бога: «Субстанция в Нем не есть собственно субстанция, но сверхсубстанция» (ibid, с. 151). О Боге можно лишь сказать, что Он есть. Тем самым не только девять категорий рассматриваются Боэцием как акциденции субстанции, но и бытие выносится за скобки любой категории, поскольку бытие присуще каждой из них: «Глагол “есть” говорится обо всех одинаково, но при этом им всем присуща не какая-то одинаковая субстанция или природа, но только имя» (ibid, с. 12). Тем самым можно говорить об одном субъекте, обладающем существованием – Боге. Бытие и есть Бог, оно не поддается категориальному определению, а все остальные категории — лишь модусы творения и рассмотрения вещи (через категории качества, количества, отношения и прочее). Бог как субъект-субстанция, обладающая бытием, воплощается в родах и видах, видовых отличиях и разнообразных признаках. Творение мыслится как различение благодаря явленности бытия Бога и благодаря обозначению именем. Категории и оказываются тем самым «механизмом» различения, которое порождает (генезис тождественен бытию) одновременно «роды сущего» и «роды обозначения».

Боэций с монохордом. Фрагмент книжной миниатюры в кембриджской рукописи, около 1150 г.

Категории у Канта

Новый этап в развитии учения о категориях связан с Кантом. Вслед за Аристотелем он объявил все категории порождением рассудка, связав каждую категорию с определенным типом суждения (например, категория общения — с разделительным суждением). Категории для него – условие возможности синтеза, то, что формирует, конституирует опыт. Категории значимы априори, предшествуют всякому опыту, выражают логические функции всех возможных суждений. Кант разделил все суждения на четыре класса и поставил им в соответствие четыре класса категорий:

Категории количества: Единство; Множество; Цельность (всеобщность).

Категории качества: Реальность; Отрицание; Ограничение.

Категории отношений: Субстанция и акциденция; Причинность и зависимость (причина и следствие); Общение (взаимодействие между действующим и подвергающимся действию).

Категории модальности: Возможность и невозможность; Существование и несуществование; Необходимость и случайность.

Методологически кантовская таблица категорий по крайней мере в трех отношениях превосходит аристотелевскую: в ней появляется отсутствовавший у Аристотеля класс модальных категорий; категории в ней не просто перечисляются, а классифицируются; гносеологическая роль категорий не сводится к разбиению всех других понятий на классы и к заданию типа связи субъекта и предиката в суждении; они трактуются как априорные формы синтеза – второго после опыта источника новых знаний. Например, подводя под категории причинности временную последовательность событий A и Б, мы трактуем A как причину Б. Этот взгляд на категории затем детально разрабатывался в неокантианстве. Таблица Канта закрепилась весьма надолго и часто еще до настоящего времени остается в своем первоначальном виде потому, что она действительно охватывает наиболее явные категории человеческого мышления.

В послекантовской философии произошел существенный сдвиг в анализе категорий – предметом исследования стали не способы предицирования, представленные в суждениях, а идеи разума, формы спекулятивных умозаключений, взаимоотношение которых выражается уже не категориями, а принципами (тождества, противоречия, его снятия в синтезе). При этом категории трактовались вне связи со структурой языка, а как нечто сущее само по себе и реализующееся в природе и человеческом духе.

В целом, методологическое осмысление неокантианцами и субъективными идеалистами функции категорий как «упорядочения данных опыта», породило два вопроса:

В чем цель такого упорядочения?

Как категории проникли в наше сознание?

Удовлетворительного ответа на них нет до сих пор. С точки зрения реалистов (материалистов и объективных идеалистов), категории, будучи формой знаний об объективной действительности, не просто упорядочивают опыт, а приводят его в более полное соответствие с этой действительностью.

Атласы архимандрита Евфимия

Овладев основами алгебры формальных аргументаций, архимандрит Евфимий стремится использовать ее для описания философско-религиозного опыта. В его изографической подаче схематические ряды контрапозиций полюсов (или «фаз») понятий соотносятся с полифонической полнотой природного и духовного мира.

«Начертание...», т. 2, с. 248

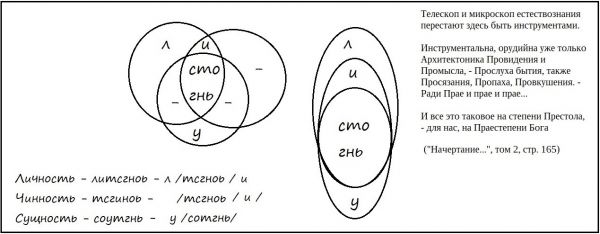
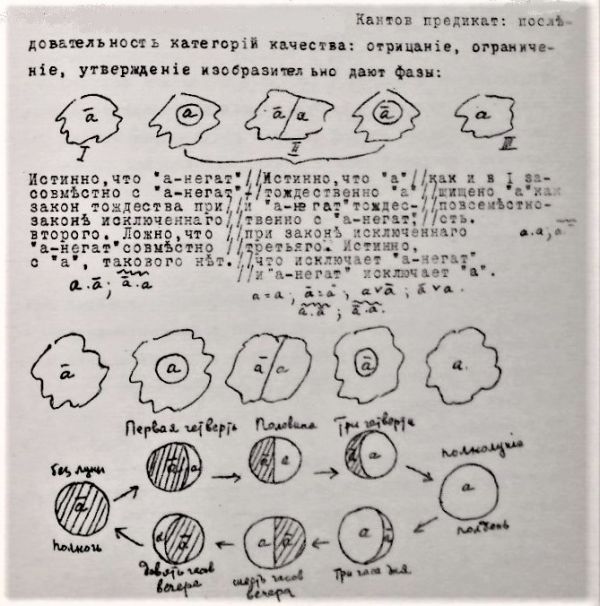
«Кантов предикат, – пишет он на странице 248 (т. 2), – <это> последовательность категорий качества – отрицание, ограничение, утверждение. Изобразительно они дают фазы: ā, ā/a, а» (см. рис.). Необходимо добавить, что во многих источниках триада кантовских категорий качества представлена как «отрицание, ограничение, реальность». Чтобы понять, почему у отца Евфимия «реальность» заменена на «утверждение», следует обратиться к «Философии имени» о. Сергия Булгакова. В частности, критикуя Канта, о. Сергий отмечает:

«Следующая дистинкция, вносимая здесь по стопам школьной логики Кантом, относится к содержанию суждения, которое может быть утверждаемо, отрицаемо, ограничиваемо (в так называемом суждении бесконечном: А есть не В); отсюда категории «реальности» (?!), отрицания, ограничения. (Спрашивается, при чем здесь реальность и что Кант разумеет под этим именем?) <...> Очевидно, что отрицание, ограничение, а также и утверждение принадлежит сфере предикативности, – продолжает о. Сергий. – Надо заметить, что утвердительных предложений, которым соответствует мнимая категория реальности, измышленная для этого Кантом, как особого вида вовсе не существует, это есть просто связка, сказуемость, функция предикативности и именования. Она всегда положительна, иной и не может быть, и отрицание или ограничение есть только частный случай утверждения. Чисто отрицательное суждение было бы уже потому невозможно, что оно разрывало бы связку, разрушало бы именование, уничтожало бы сущность суждения, вело бы к его отсутствию. В этом смысле всякое отрицание есть ограничение, отграничение, квалификация суждения, вообще реализуемо только в положительном контексте, в связи и на фоне положительных суждений. По смыслу отрицания имеют разные оттенки, которые выражаются или общим строем фразы, или отдельными словами (как в греческом языке μή, οὐ, ἀ). Во всяком случае, отрицание исходит из предшествующего или подразумеваемого положительного суждения, есть как бы его зачеркивание. Поэтому оно есть функция положительного суждения, его разновидность, или частный случай».

И далее, там же: «...В языке, в речи и мысли, пространственность и временность выражаются в предикативной функции как ее известная окраска или качество. Поэтому они имеют свою границу, суть частный случай этой предикативности, его квалификации, но отнюдь не составляют всеобщей формы познания, рамы для всякой мысли. Кант неправ относительно языка, так же как неправ он относительно мысли и познания. Если бы он прислушался здесь к показанию самой мысли-слова, он не стал бы исходным пунктом своего построения брать интуиции времени и пространства как самую всеобщую форму познания, ибо она вовсе не является всеобщей, но взял бы анализ предикативности или предложения, именования. Тогда он был бы освобожден от целого ряда проблем и трудностей, возникающих на этом его пути» ([Булгаков ФИ 98]). «Почти всю свою таблицу категорий Кант мог бы вывести из спряжения, хотя здесь они располагаются иначе, чем в его изложении, ибо живая «рапсодия» (по его же выражению, примененному к таблице категорий из Аристотеля, Пролегомены, 103) языка не сходится с формальным и отнюдь не бесспорным расположением их у Канта. Кант все категории отнес к связке, вне ее он не знает применения своих категорий. Язык, который не считается с запретами Канта, вмещает категории не только в спряжение, но и в склонение. Что в самом деле представляет собой число, как не категорию количества (и притом в трех его кантовских формах: единство, множественность и всеобщность или целостность)? Что представляет собой творительный падеж, как не категорию причинности, а другие падежи — в известных соединениях родительный (разделительный), дательный, предложный — что иное, как не взаимодействие, а именительный, как мы уже знаем, субстанцию? В соединении же с предлогами, частицами, словами разные падежи способны передавать оттенки разных категорий, являясь так называемыми «обстоятельствами» или косвенными дополнениями и определяя место, время, образ действия» [Булгаков ФИ 110-111].

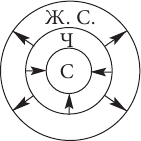
«Фазовые изменения, – пишет о. Евфимий, комментируя рисунок на стр. 248, – столько же теория, сколько и натура! А вслед за натурой логические законы мышления блюдут и Сам Религиозный Символ Натуры! “Се жених грядет в полунощи” с первой же секунды прибавления света. “Христос рождается, славите” с первой же секундой по самой длинной ночи в году. “Демон полуденный” приражается с первой же секундой уменьшения света. В этих Пунктах суточных и годовых действителен Закон Исключенного Второго! И Литургию совершают навстречу солнца, до полдня, а не при убывающей солярности! И Религиозный Символ Натуры требует точного календаря. Две величины, например, небо и земля, находящиеся по кругу в фазовых изменениях, в своих соотношениях и образуют в исчерпании 16 умыслообразов, причем сама их последовательность, указываемая Таблицей Исчерпания, уже есть Закон Значимого Бытия».

Атлас 22

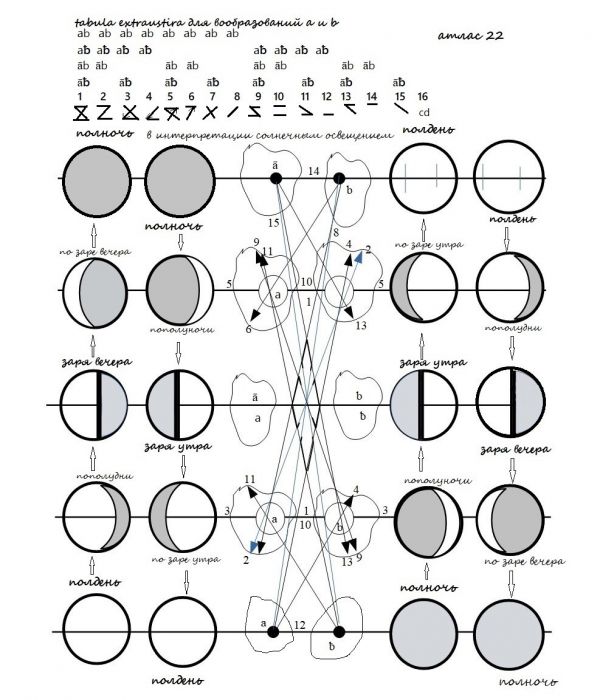
Основы схематизации всего сущего – мироздания, явлений природы и т. п., вплоть до божественных предопределений – были заложены в математических трудах польского мессианиста Юзефа Гоэнэ-Вронского (1776–1853). Архимандрит Евфимий осуществил своеобразное развитие этих идей, попытавшись приживить их на почву православной догматики. Ниже мы воспроизводим одну из рукописных схем о. Евфимия, на которой представлена партитура смены дня и ночи «в интерпретации солнечным светом»:

«Начертание...», т. 1, атлас 22

Как уже упоминалось в главе I, tabula exhaustive – исчерпывающая таблица. Градации освещенности заданы здесь как комбинаторные сочетания света (Солнце) и тьмы (Луна). Очевидно, что в зависимости от геолокализации и времени года, а также с учетом разнообразных природных флуктуаций Солнце и Луна могут существенно отклоняться от заявленных в партитуре соотношений (сюда не вписывается, например, полярная ночь). Но в данной схеме импонирует прежде всего демиургический размах ее создателя, а что же касается нюансов... они остаются, так сказать, ad libitum.

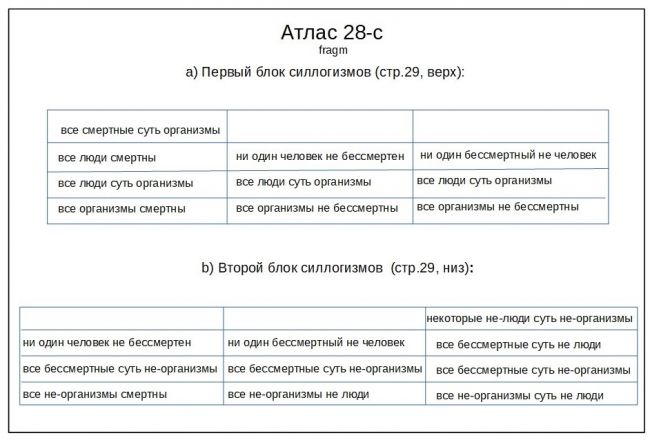
Атласы 27 и 28. Силлогизмы о Сократе и бессмертии

Россыпи силлогизмов разбросаны по всему трактату о. Евфимия, но особенно много их в первом томе (стр. 26-40, Aтласы 27 и 28 etc). Ввиду крайне неудовлетворительного качества имеющихся в нашем распоряжении копий трактата «Начертание...», на первом этапе исследовательской работы нам пришлось заняться черчением, перерисовывая набело схемы и атласы архимандрита Евфимия. Ниже, для сравнения, мы помещаем исходные клише атласов 27 и 28 (в том виде, в котором они наличествуют в трактате) и скопированные нами версии этих атласов.

«Начертание...», т. 1, атлас 27 (оригинал)

Представленные в 27 и 28 Атласах «схолии» выглядят как многоуровневые логико-изографическая импровизации, вдохновленные самым расхожим иллюстративным примером из аристотелевой аналитики: «Все люди смертны; Сократ человек; (значит) Сократ – смертен».

«Начертание...», т. 1, атлас 27 (перерисованная нами версия)

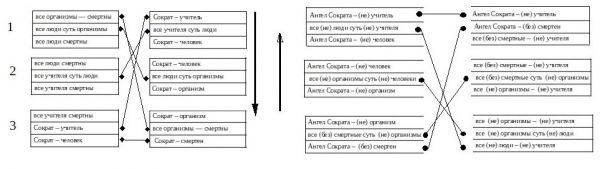
«Векторные» конструкции в нижней части Атласа 27 напоминают так называемые логические цепочки. Если понятие «Сократ» последовательно обобщается (Сократ → учителя → люди → организмы → смертные), то понятие «Ангел Сократа» – ограничивается (Ангел Сократа → бессмертные → не организмы → не люди → не учителя).

На стр. 249 первого тома о. Евфимий указывает:

«Двойственность обособления contrepositia крайних фаз одной и той же величины приводит к двойственности во взаимоотношении двух величин. Если взять неотвязно навязывающийся знаменитый пример “все люди смертны”, то в обращении получим: “все бессмертные нечеловечны”. На чертеже показаны как вывод из силлогизма, средним термином которого взят “организм” (ƅ ) и “неорганизм” (ƀ)».

«Начертание...», т. 1, чертеж со стр. 249 (оригинал)

В данном чертеже архимандрит Евфимий воспользовался алгеброй логики (или Булевой алгеброй). Два уравнения, записанных здесь построены исключительно на импликации. Импликация (лат. Implisito – тесно связываю) – это логическая операция, соединяющая два высказывания при помощи связки «если..., то» в сложное высказывание, которое символически обозначается с помощью знака → (А → В) и читается: «если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяется также знак ⊃ (A ⊃ B). Пример импликации: «Если полученный четырехугольник квадрат, то около него можно описать окружность» (ссылка на справочные материалы, pdf-online, открыть в новом окне): | Таблицы истинности и логические схемы . В нашем случае первая строка уравнения соответствует следующим высказываниям: «если люди – организмы» (a ⊃ b) и «если организмы – смертны» (b ⊃ c), из этого следует, что «люди – смертны» (a ⊃ c). Вторая строка гласит: «если бессмертные – не организмы, и если организмы нечеловечны, то бессмертых следует признать нечеловечными». Весьма странное умозаключение!

«Если ограничение, или остров, или полюс a мы будем рассматривать в сторону количественного уменьшения, – продолжает о. Евфимий, – то мы придем к выводу: Сократ бессмертен. Но и полюс ĉ может дать нам соотносительно, что какой-то олдин бессмертный, сдруженный Сократу, нечеловечен. И как результат: Сократ не есть его ангел хранитель, и ангел хранитель не есть Сократ (у ангелов нет смертного тела)! Для взаимоотношений неба и земли пример этот только один из 16 умыслообразов этих взаимоотношений, а именно, несовместимость, incompatibilitas. Здесь организмы несовместны с бессмертными, неорганизмы с людьми, люди с бессмертными, в конце концов, Сократ со своим ангелом. Но люди и живы и бессмертны по душе. И судьба их целостного бессмертия, как судьба взаимоотношений неба и земли, решается во всей целокупности 16 умыслообразов, т. е. в Целом Энергемы Значимого Бытия» («Начертание...», т. 1, стр. 250).

«Начертание...», т. 1, атлас 28 (оригинал)

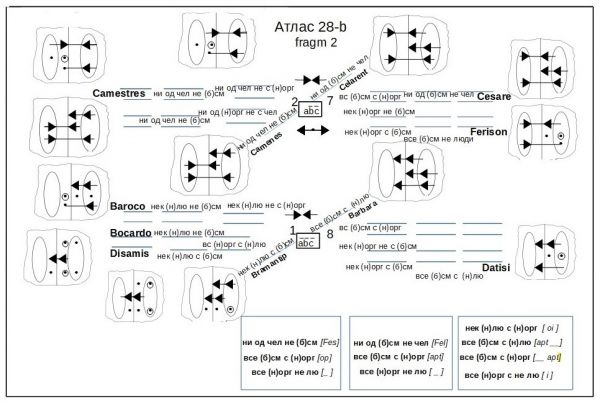
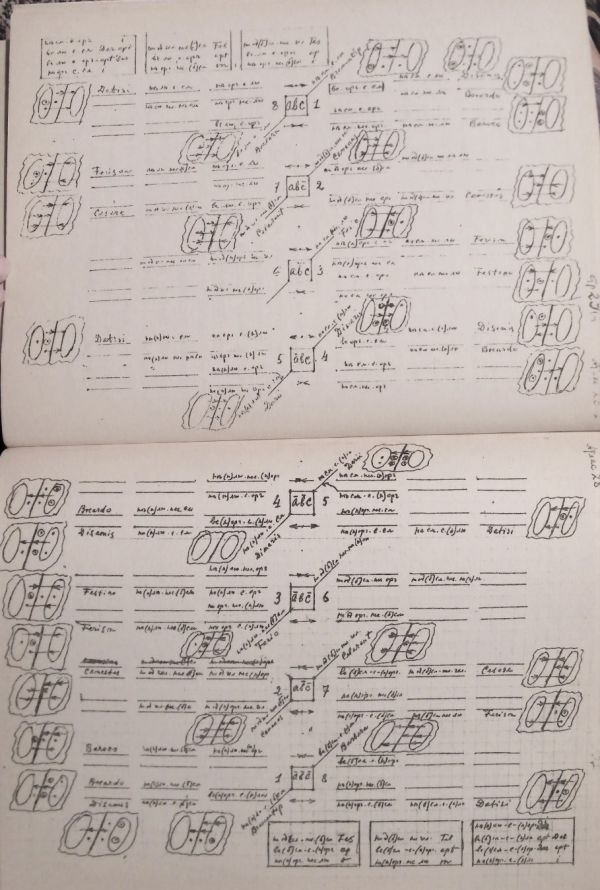
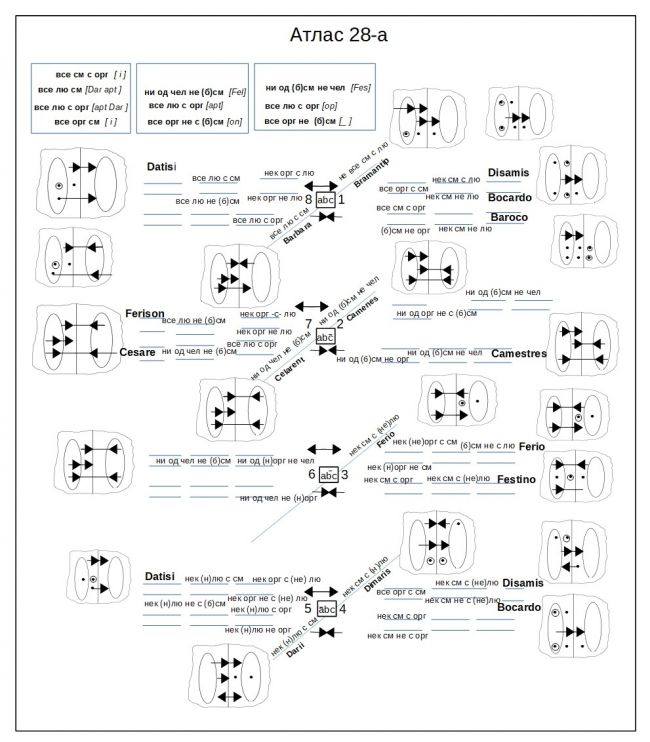
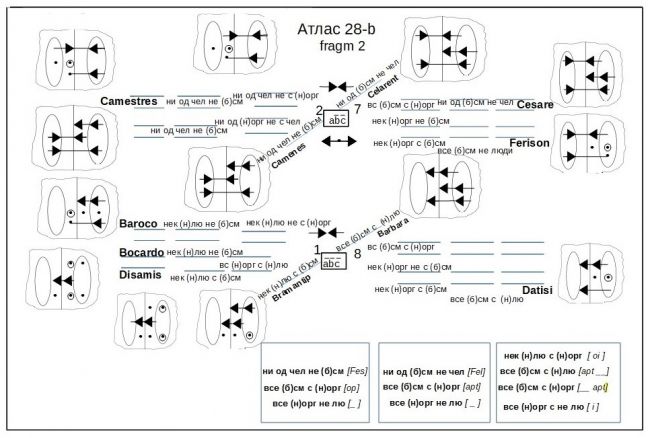
На фоне прочих чертежей и схем трактата «Начертание...» Атлас 28 – самый «нечитабельный», самый сложный. Информация, которую архимандрит Евфимий попытался вложить в двухстраничный разворот, вряд ли разместилась бы и на десяти страницах. Если внимательно приглядеться к Атласу, можно разобрать мнемонические кодовые имена фигур силлогизмов: Barbara, Darii etc.

«Начертание...», т. 1, атлас 28 (оригинал, вторая страница)

При изучении неразборчивых помет и не поддающихся дешифровке сокращений невольно приходят на ум слова историка старообрядчества И. В. Сагнака: «Чтение рукописи-автографа, в особенности, если она написана "сложным" индивидуальным почерком – это всегда исключительно творческий, во многом мистически (иначе не скажешь!) организованный процесс, основанный в высочайшей степени на глубокой "эмпатии" соучастников этого загадочнейшего и прекраснейшего действа. <...> Многолетние опыт и практика чтения именно таких, – сложных, выглядящих порою просто как некая "кардиограмма", но принадлежащих людям недюжинным, – почерков одаряют ... незабываемыми и ни с чем не сравнимыми переживаниями редчайшего сродства – и душевного, и умственного – с людьми, водившими когда-то пером по бумаге».

«Начертание...», т. 1, Атлас 28 (верхний лист; перерисованная версия)

«Начертание...», т. 1, Атлас 28 (нижний лист, часть 1; перерисованная версия)

«Начертание...», т. 1, Атлас 28 (нижний лист, часть 2; перерисованная версия)

«Начертание...», т. 1. Расшифровка верхнего и нижнего блоков силлогизмов атласа 28

Столбцы и таблицы

В некоторых случаях (например, на стр. 31 первого тома) силлогизмы сгруппированы в столбцы:

вс орг – см вс лю с орг вс лю – см Сокр – уч вс уч с лю Сокр – чел etc

Так – в сокращенном виде – силлогизмы прописаны в манускрипте отца Евфимия. Ниже приводится предположительная расшифровка сокращений. Дело в том, что свой манускрипт о. Евфимий размножал на ротаторе, в итоге многие слова и сокращения оказались нечитабельными (например, в оригинале пометки «вс» /все/ и «нек» /некоторые/ были практически неотличимы друг от друга).

«Начертание...», т. 1, стр. 31 (фрагм.: нисходящие, "катаболические" столбцы силлогизмов)

«Начертание...», т. 1, стр. 31 (фрагм.: восходящие, "анагогические" столбцы силлогизмов)

«Начертание...», т. 1, стр. 31 (нисходящие и восходящие столбцы силлогизмов)

Для удобства чтения эти группы утверждений можно свести в таблицу:

Вместо заключения

Некоторые страницы трактата прямо-таки перенасыщены атрибутикой, исторически сложившейся в недрах науки о мышлении: здесь и субституты теории множеств, и логический квадрат, и мнемоны (Barbara, Bocardo, Darii etc), изобретенные Михаилом Пселлом для обозначения модусов разного типа суждений… Но насколько корректно воспользовался архимандрит Евфимий данным инструментарием? Вопрос остается открытым.

Библиография

[Библер Кантовская критика] – В. С. Библер. Кантовская критика способности суждения. Парадоксы схематизируются в антиномии. – https://fil.wikireading.ru/17805.

[Боэций 1990] – Боэций. Утешение философией и другие трактаты. – М., 1990.

[Богатырев 2016] – https://wikilivres.ru/Архимандрит_Евфимий_и_Казанский_храм_(Богатырев).

[Бочаров и др. 2019] – Бочаров В., Ивин А., Бернштейн В. Силлогизм (Гуманитарная энциклопедия, раздел: Концепты научного дискурса). – https://gtmarket.ru/concepts/7011.

[Булгаков ФИ III] – С. Булгаков. Философия имени. III. К философии грамматики. – http://ivashek.com/fr/172-chapters/filosofiya-imeni/598-iii-k-filosofii-grammatiki.

[Гусев 2015] – Д. А. Гусев. Логика. – М., Прометей, 2015. – https://e-libra.su/read/515303-logika-uchebnoe-posobie.html.

[Канаева iphras.ru] – Н. А. Канаева. Эволюция концепции индийской логики у Ф. И. Щербатского (на материале сравнения книг «Buddhist Logic» и «Теория познания и логика по учению позднейших буддистов»). – https://iphras.ru/uplfile/root/biblio/hp/hp18/1.pdf.

[Кант 1994] – Кант И. Критика чистого разума. Пер. Н. Лосского, ред. Ц. Арзаканян и М. Иткин. – М.: Мысль, 1994.

[Конт-Спонвиль 2012] – Андре Конт-Спонвиль. Философский словарь. – М., Этерна, 2012 (Категория).

[Кузичев 1968 25] – Кузичев А. Диаграммы Венна. История и применения. — М.: Наука, 1968, с. 25.

[Левин и др. Категория] – Г. Д. Левин, А. П. Огурцов, В. А. Эдельман. Категория. / Гуманитарная энциклопедия: Концепты [Электронный ресурс] // Центр гуманитарных технологий, 2002–2020 (последняя редакция: 27.06.2020). URL: https://gtmarket.ru/concepts/6880.

[Лурье 2006] – Лурье В. М. История византийской философии. Формативный период. — СПб., Axioma, 2006. XX + 553 с., Раздел 2, гл. 1. – http://www.hgr.narod.ru/div2ch1.htm.

[Таблицы истинности (synergy.ru, pdf-online)] – Таблицы истинности и логические схемы. Учебное пособие с сайта synergy.ru (pdf, 35 стр.). – https://synergy.ru/assets/upload/news/articles_ege/ege/informatika/19%D0%A2%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D1%8B%20%D0%B8%D1%81%D1%82%D0%B8%D0%BD%D0%BD%D0%BE%D1%81%D1%82%D0%B8%20%D0%B8%20%D0%BB%D0%BE%D0%B3%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5%20%D1%81%D1%85%D0%B5%D0%BC%D1%8B.pdf.

[Лосский Вл. Н. 1991 Гл. 14. Воплощение] – Лосский В. Н. Очерк мистич. богосл. вост. Церкви. – Догматическое богословие. — М., 1991.

[Начертание] — Евфимий (Вендт), архимандрит. Начертание и наречение решений Отрешенного. Графика и грамматика Догмата. Рукопись в 3 тт., 25 (?) экз. Муазне, 1968-1973.

[Павлинов 2015] – И. Я. Павлинов. Номенклатура в систематике. История, теория, практика. — М., КМК, 2015. – http://ashipunov.info/shipunov/school/books/pavlinov2015_nomenkl_v_sistematike.pdf или https://www.webcitation.org/6oeE0p0P4.

[Парфенова Органон] – Парфенова Е. Г. Органон. – На сайте: Электронная библиотека ИФ РАН. Новая философская энциклопедия. – https://iphlib.ru/library/collection/newphilenc/document/HASHec864c32308ba71ae4f8ec.

[Правосл. Энц. т. 24 628-647] – Свящ. Василий Лакомкин, Беневич Г. И. Иоанн Филопон. – Православная энциклопедия, т. 24, стр. 628-647. – на сайте: Электронная библиотека ИФ РАН. Новая философская энциклопедия. – http://www.pravenc.ru/text/471531.html.

[Попова, Пушкарский, Чалый 2012] – В. С. Попова, А. Г. Пушкарский, В. А. Чалый. Онтология в метафизике versus онтологии в теориях аргументации. – Рацио.ru. 2012. № 8, стр. 109. – https://journals.kantiana.ru/upload/iblock/121/Попова,%20Пушкарский,%20Чалый_99-126.pdf.

[Радлов 1900] – Радлов Э. Л. Силлогизм // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907. – https://ru.wikisource.org/wiki/ЭСБЕ/Силлогизм.

[Свинцов 1998] – В. И. Свинцов. Логика. Элементарный курс для гуманитарных специальностей. – М.: Скорина, 1998.

[Стяжкин 1967] – Стяжкин Н.И. Формирование математической логики. М.: Наука, 1967.

[Субботин ФЭ т. 2, 74] – А. Л. Субботин. Древо Порфирия // Философская энциклопедия : в 5 т. / глав. ред. Ф. В. Константинов. — М. : Сов. Энц., 1962. — Т. 2 : Дизъюкция — комическое. — С. 74.

[Таблицы истинности (synergy.ru, pdf-online)] – Таблицы истинности и логические схемы. Учебное пособие с сайта synergy.ru (pdf, 35 стр.). – https://synergy.ru/assets/upload/news/articles_ege/ege/informatika/19%D0%A2%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D1%8B%20%D0%B8%D1%81%D1%82%D0%B8%D0%BD%D0%BD%D0%BE%D1%81%D1%82%D0%B8%20%D0%B8%20%D0%BB%D0%BE%D0%B3%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5%20%D1%81%D1%85%D0%B5%D0%BC%D1%8B.pdf.

[Эйкалович 1973] – Эйкалович Г. Развернутый иероглиф. Памяти архимандрита Евфимия Вендта. – Вестник РСХД, №107 (1), 1973.

[Hazewinkel 2002] – Michiel Hazewinkel. Venn diagram. – Encyclopædia of Mathematics, Springer, 2002. – https://fr.wikipedia.org/wiki/Michiel_Hazewinkel.

[Smith Aristotle's Logic] – Robin Smith. Aristotle's Logic. – Stanford Encyclopedia of Philosophy. – https://plato.stanford.edu/entries/aristotle-logic. https://ru.wikisource.org/wiki/ЭСБЕ/Пселл,_Михаил.

Примечания

Copyright © Михаил Богатырев, 30 июня 2020, Париж